洛谷P7745 [COCI2011-2012#3] ROBOT 题解
题目传送门
调了两个月终于调出来了
首先看数据范围: 且
纯根据题意模拟的 肯定过不了
这时候就需要预处理。
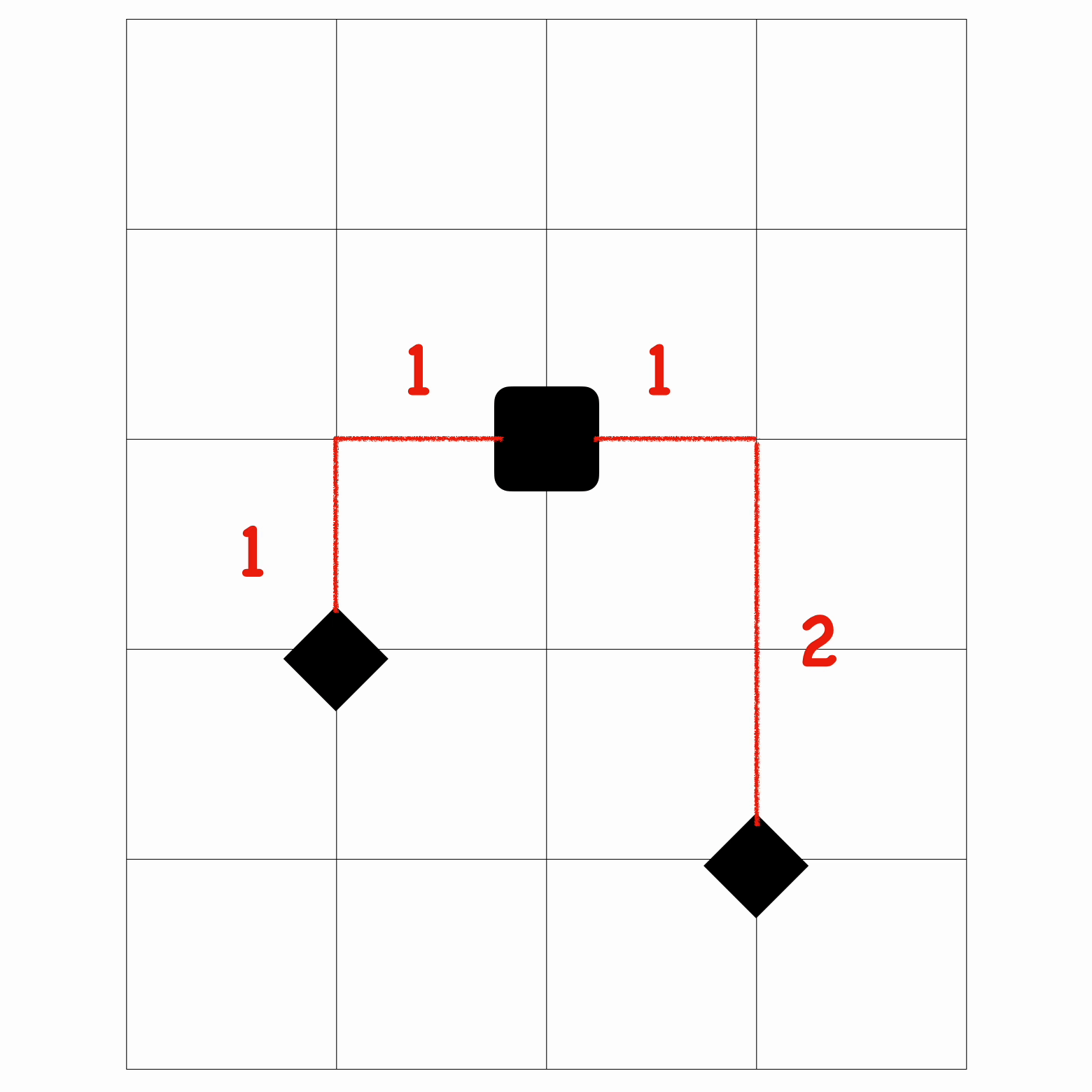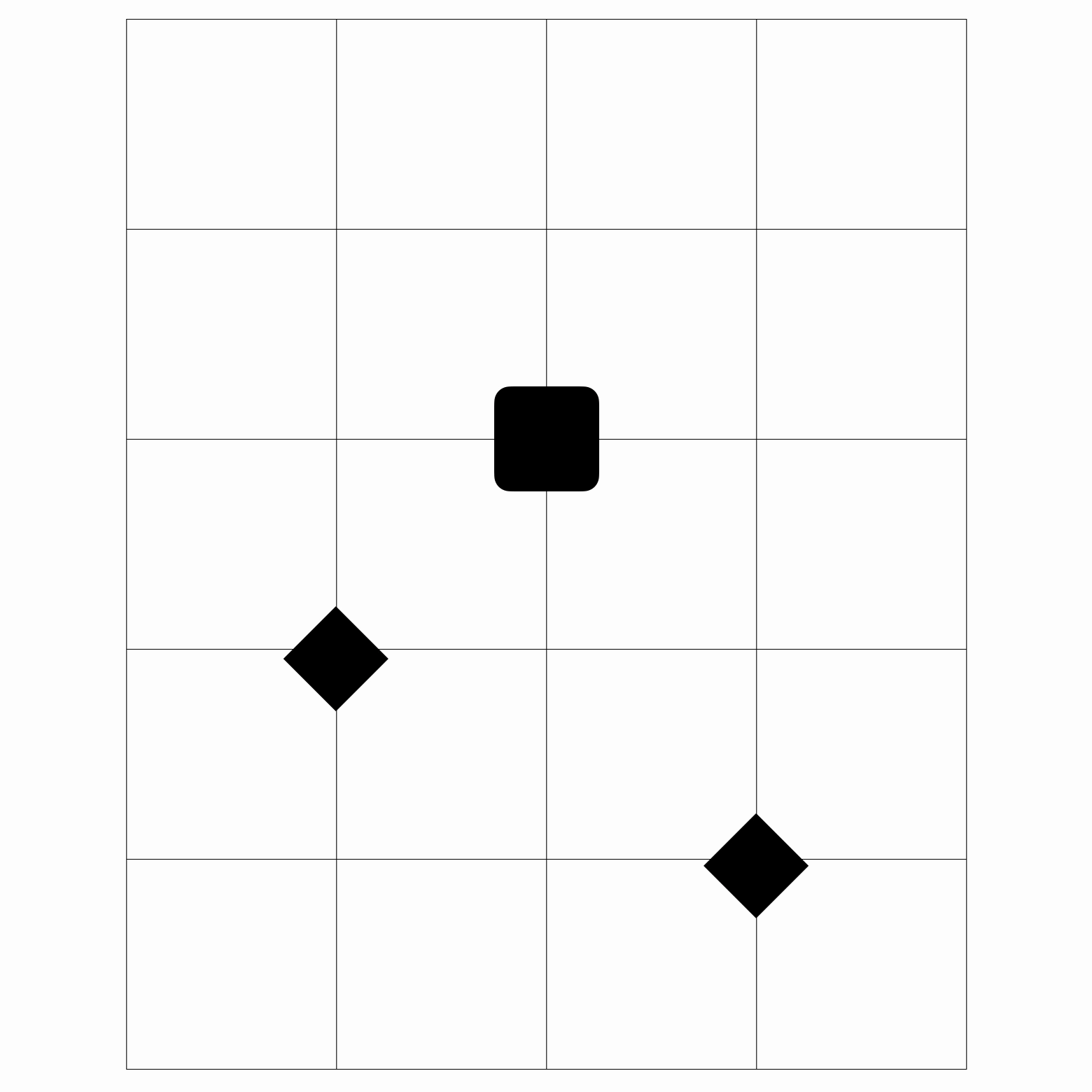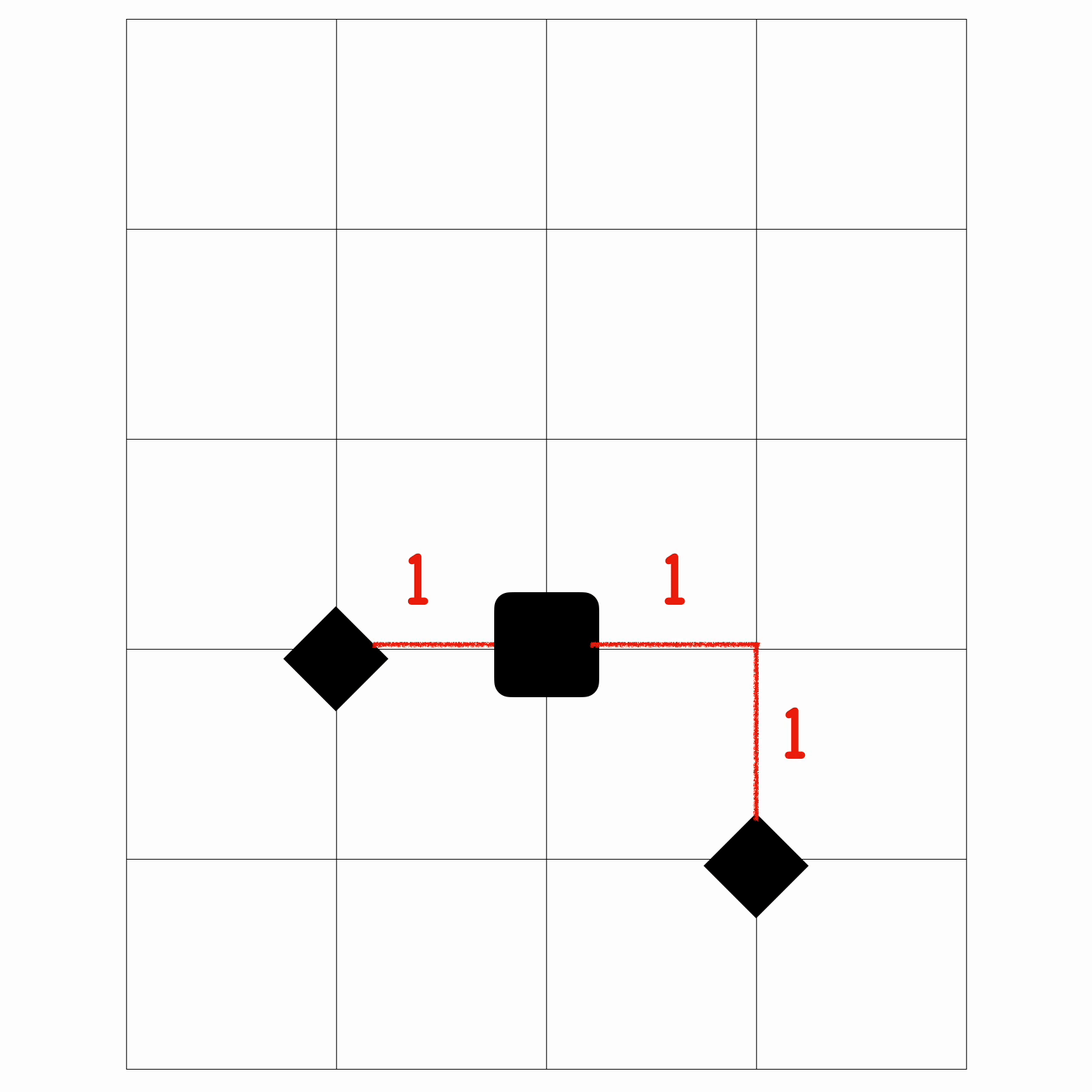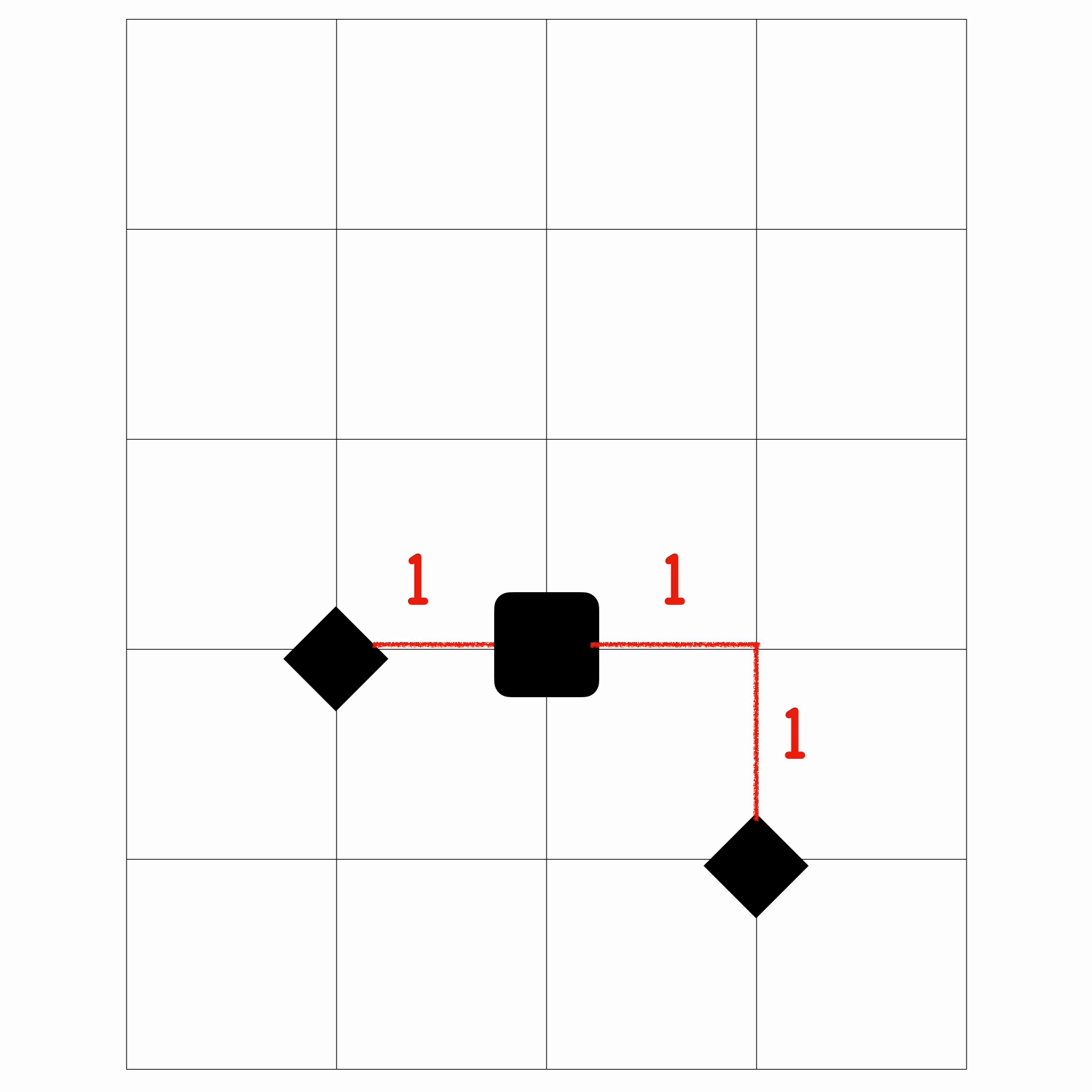
对于曼哈顿距离,我们可以把它想象成一个点到另一个点的最短路,这边放个图例来方便理解
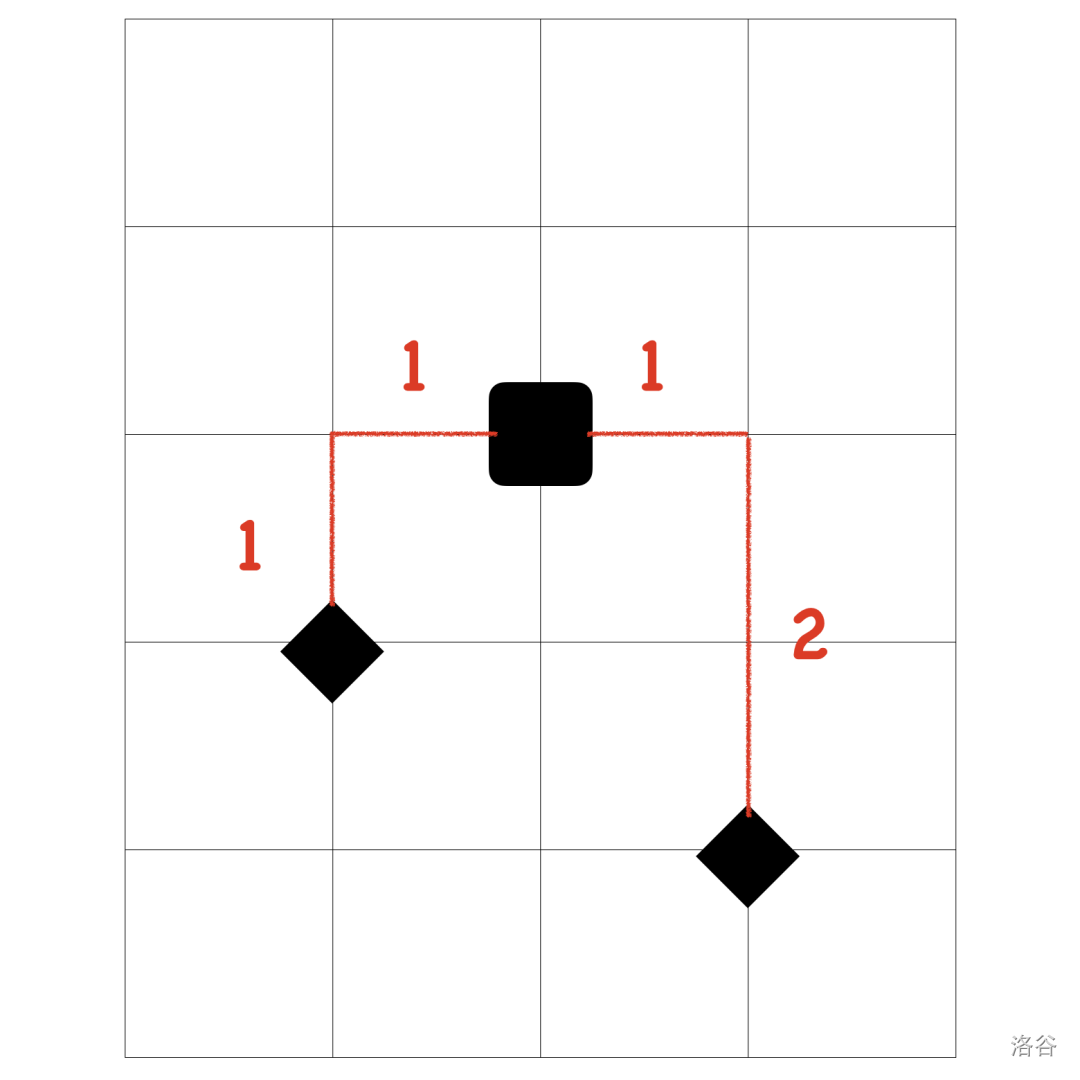
如图,容易发现:
图上 轴距离和为 $1+1=2$ , 轴距离和为$1+2=3$
, 轴距离和相加即为两个控制点到 ROBOT 的曼哈顿距离。
一提到预处理,首先我们想到的是前缀和。
求数组前缀和的方式十分简单,仅需要写一个循环,例如下方代码:
1 | |
在得到前缀和后,根据题意,容易得出每次移动对于每个控制点到ROBOT的距离 $+1$ 或 $-1$ ,我们只需要详细写出 $+1$ 或 $-1$ 即可。
同样的,这边放一个 gif 来演示收到 “J” 指令是的操作情况。
(如果 gif 挂了请@或私信我)
举例当指令为 “S” 时:
1 | |
在一系列例如上方的处理后,我们仅需要提前(在输入每个机器人坐标时)算出初始距离,并对这个初始距离进行加减即可。
写完后发现时间复杂度仅有 ,可以轻松通过
当然,此题也可以用 STL 中的 lower_bound 和 upper_bound 写。
需要注意的是,为防止数组下标为负数,需要给每一个数组下标都加一个常量!!!
本博客所有文章除特别声明外,均采用 CC BY-NC 4.0 协议 ,转载请注明出处!